Mixture-of-Subspaces in Low-Rank Adaptation

论文：https://arxiv.org/abs/2405.15179

github:https://github.com/wutaiqiang/MoSLoRA

 背景

LoRA 通过在预训练权重上添加低秩分支来进行微调，从而减少了需要更新的参数量。然而，LoRA 在适应复杂任务时仍有局限性，主要在于其无法充分捕捉子空间之间更复杂的关系。为了提升性能，探索如何更好地混合这些低秩子空间的信息。

为了解决 LoRA 的不足，研究人员提出了一种新的子空间混合方法——Mixture-of-Subspaces LoRA (MoSLoRA)。MoSLoRA 通过引入一个可学习的混合器来融合多个子空间，从而灵活地捕捉更多信息。这种方法在多个基准测试中表现优异，显著提升了模型的鲁棒性和准确性，同时引入的额外参数和计算开销可以忽略不计

方法论

第一个表达式 x(A1B1 + A2B2)：

• 这里使用的是传统的 LoRA 分解方式，即将矩阵 A 分解为两个子空间 A1 和 A2，矩阵 B 分解为 B1 和 B2。

• 然后，分别在子空间内进行相乘（A1 与 B1，A2 与 B2），再将结果相加。

• 这种方法在保持模型参数减少的同时，还能有效保持一定的模型表现。

第二个表达式 x(A1B1 + A2B2 + A1B2 + A2B1)：

• 这是在“Mixing Two Subspaces”策略下引入的一种新方法。

• 不仅包含了原始的乘积（A1B1 和 A2B2），还增加了交叉项（A1B2 和 A2B1）。

• 这些额外的交叉项旨在探索更复杂的组合方式，可能会捕捉到更多的特征关系，从而提升模型的表现。

# 低秩适应 (LoRA) 方法对比

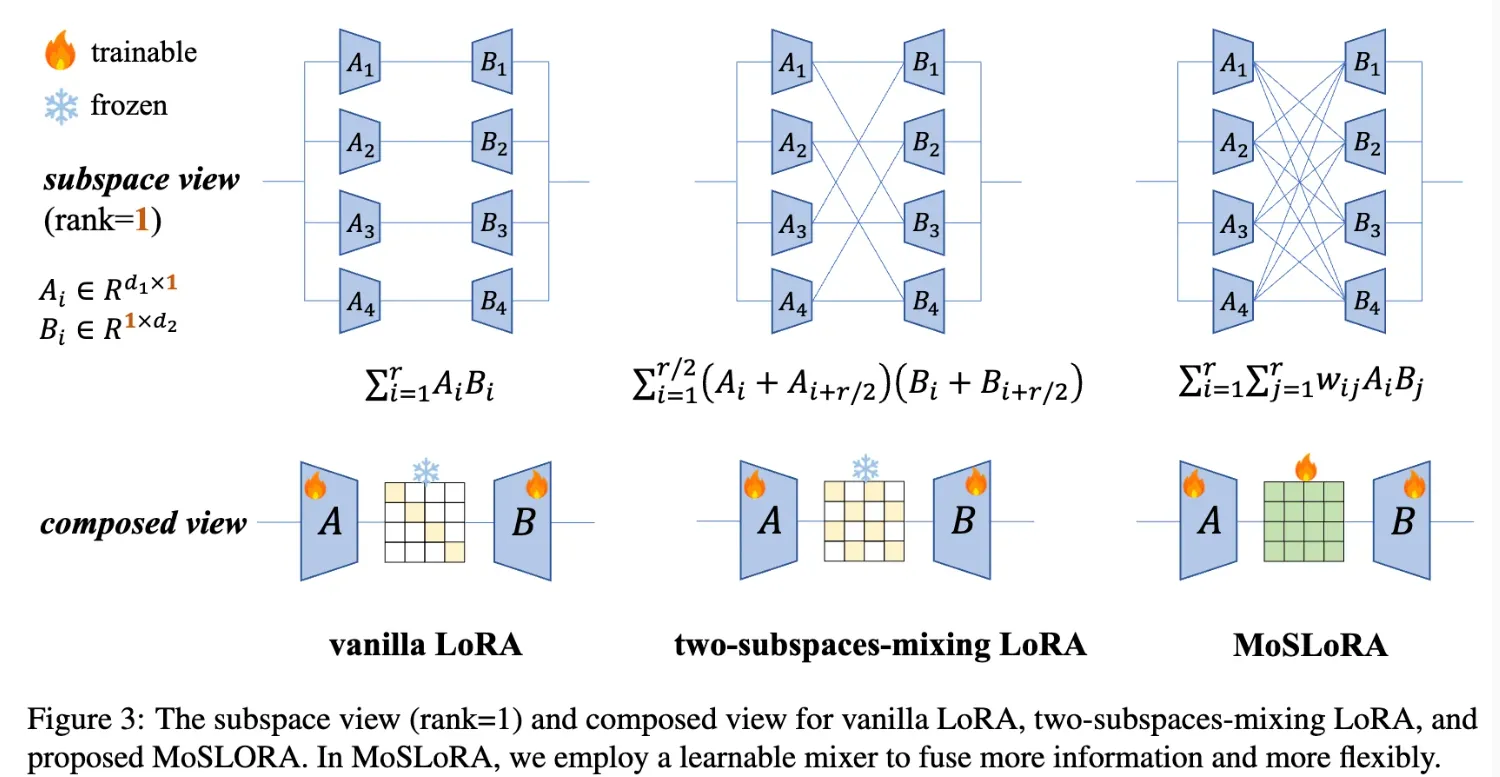
## 1. Vanilla LoRA

最基本的低秩适应方法。

公式：

```

∑(i=1 to r) Ai * Bi

```

其中，Ai ∈ R^(d1×1)，Bi ∈ R^(1×d2)，r 是秩。

特点：简单直接，但信息交互有限。

## 2. Two-subspaces-mixing LoRA

通过混合相邻子空间增强信息交流。

公式：

```

∑(i=1 to r/2) (Ai + Ai+r/2) * (Bi + Bi+r/2)

```

特点：每对相邻子空间（如 A1 和 A3，B1 和 B3）进行混合，增加信息交互。

## 3. MoSLoRA (Proposed)

引入可学习的混合器来融合更多信息。

公式：

```

∑(i=1 to r) ∑(j=1 to r) wij * Ai * Bj

```

其中，wij 是可学习的权重。

特点：最灵活，允许所有 Ai 和 Bj 之间的交互，可学习最优混合策略。

## 组合视图对比

- **Vanilla LoRA**: A 和 B 之间是固定连接。

- **Two-subspaces-mixing LoRA**: A 和 B 之间有固定混合模式。

- **MoSLoRA**: A 和 B 之间有可训练混合器，允许更灵活的信息融合。

MoSLoRA 的主要优势在于其灵活性和学习能力，可根据具体任务自适应调整子空间交互，潜在获得更好性能。