LLama系列模型架构分析

大家好，我是 Bob! 😊 一个想和大家慢慢变富的 AI 程序员💸 分享 AI 前沿技术、项目经验、面试技巧! 欢迎关注我，一起探索，一起破圈！💪

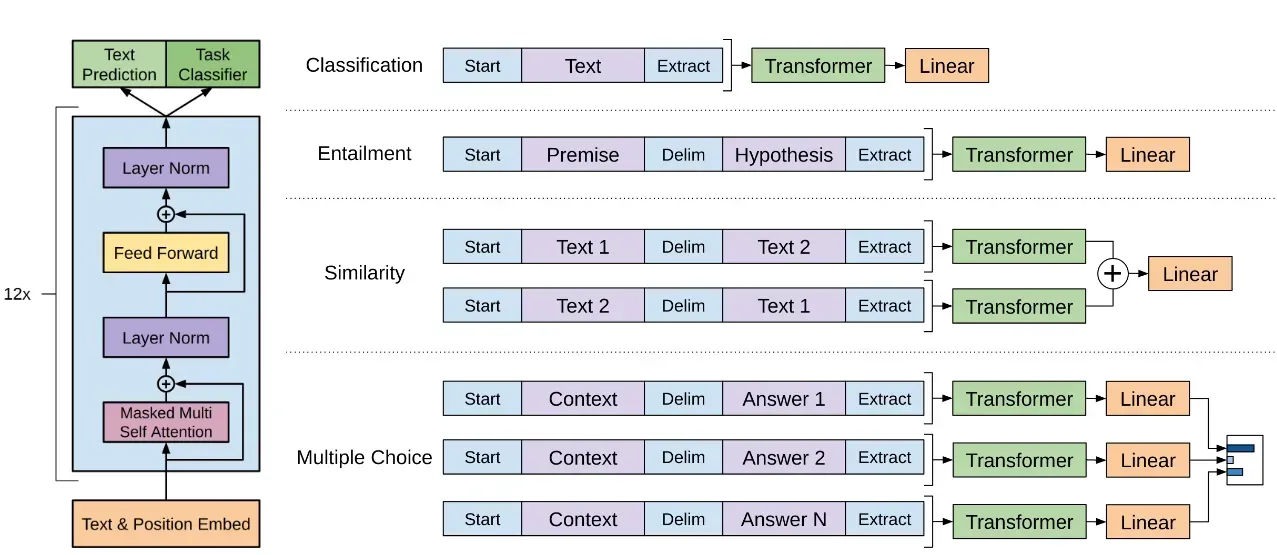
首先回忆一下gpt架构。主流的大语言模型几乎都是由生成式GPT改进而来

LLama3

相较与GPT2的模型架构还是有改进的：

位置编码：去除了绝对位置编码，采用了旋转位置编码RoPE,可以兼顾相对位置和绝对位置的信息以提高模型的泛化能力。

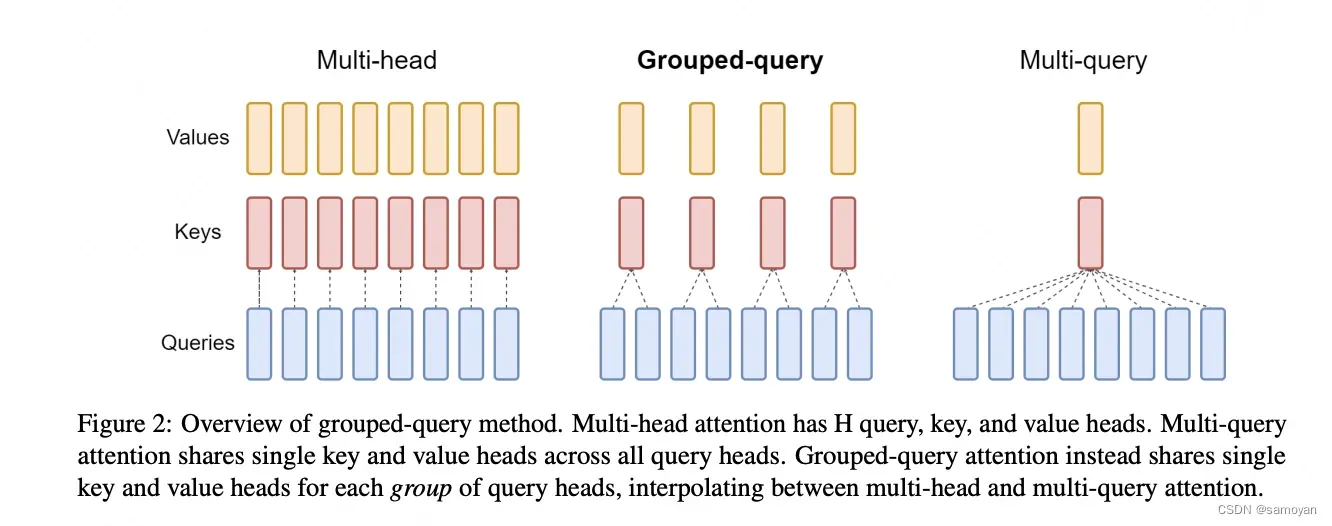
分组查询注意力 (GQA):8B 和 70B 的LLaMA3都采用了分组查询注意力 (GQA)机制，将Query进行分组，组内共享KV，使得K和V的预测可以跨多个头共享，显著降低计算和内存需求，提升推理速度。

RMSNorm & Pre-normalization：使用RMSNorm均方根归一化函数。作用：为提升训练稳定性，LLaMa对每个Transformer的子层的输入进行归一化，而不是对输出进行归一化。用pre layer Norm(预训练层归一化),去除layer normalization中偏置项。

激活函数：没有采用ReLU激活函数，而是采用了SwiGLU激活函数（结合SWISH 和 GLU 两种者的特点）。SwiGLU 主要是为了提升 Transformer 中的 FFN(feed-forward network) 层的实现。FFN通常有两个权重矩阵，先将向量从维度d升维到中间维度4d，再从4d降维到d。而使用SwiGLU激活函数的FFN增加了一个权重矩阵，共有三个权重矩阵，为了保持参数量一致，中间维度采用了 2/3 x4d ，而不是4d。

AdamW优化器:使用了AdamW优化器，并使用cosine learning rate schedule

技术实现

RoPE

我们可以思考一下，如何表达出两个张量之间的匹配度。如attention的论文所表示的，使用q k的内积再做softmax来表示。而为了加入位置信息，使用sin/cos的绝对位置编码，加入张量以影响内及大小/匹配度。但是这样某种意义上来说并没有什么意义，还会改变语义信息。

但改变内积还有一种方法，就是保证原有q k的值不变，改变张良之间的夹角。夹角越小，匹配度越高。

这时候假设输入序列为2维，引入旋转矩阵计算q（旋转mθ），同样也可以计算k(nθ)。那么从相对的角度上来说,某一个向量旋转了（mθ-nθ）。

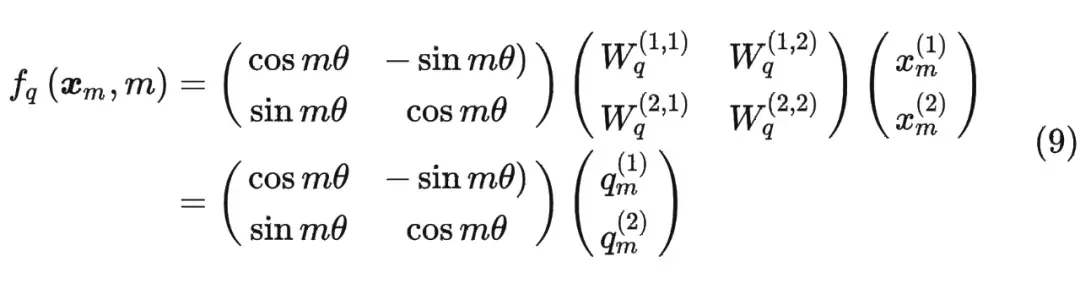
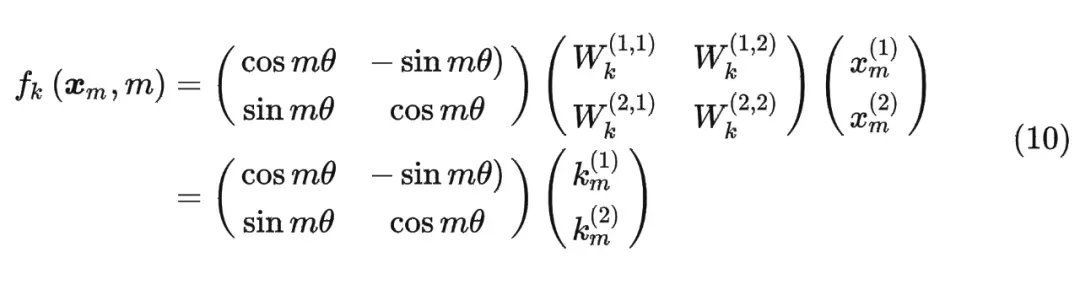
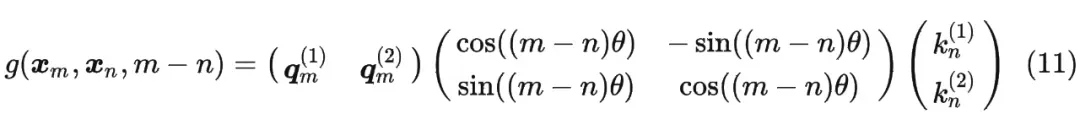
内积满足线性叠加性，因此任意偶数维的 RoPE，我们都可以表示为二维情形的拼接，即

但是这种矩阵计算不高效，浪费算力，我们做这种修改

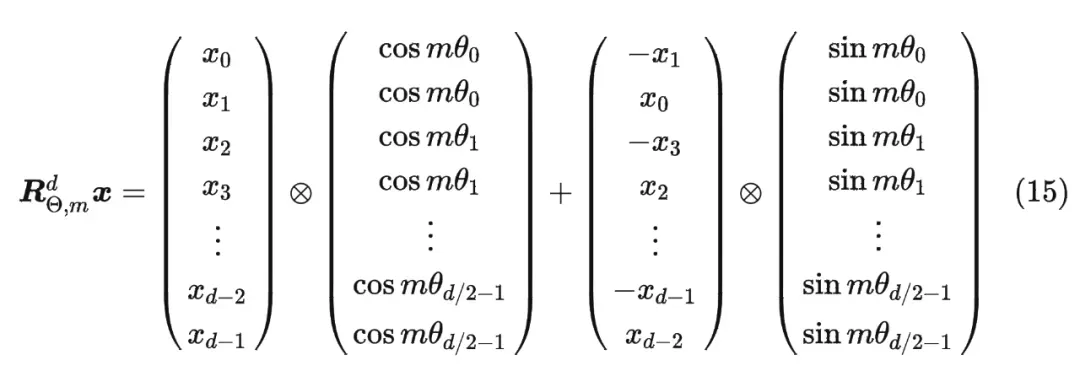
代码：

python
import torch

def precompute_freqs_cis(dim: int, end: int, constant: float = 10000.0):
    '''
    计算cos和sin的值，cos值在实部，sin值在虚部，类似于 cosx+j*sinx
    :param dim: q,k,v的最后一维，一般为emb_dim/head_num
    :param end: 句长length
    :param constant： 这里指10000
    :return:
    复数计算 torch.polar(a, t)输出， a*(cos(t)+j*sin(t))
    '''
    # freqs: 计算 1/(10000^(2i/d) )，将结果作为参数theta
    # 形式化为 [theta_0, theta_1, ..., theta_(d/2-1)]
    freqs = 1.0 / (constant ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim)) # [d/2]

    # 计算m
    t = torch.arange(end, device=freqs.device)  # [length]
    # 计算m*theta
    freqs = torch.outer(t, freqs).float()  # [length, d/2]
    # freqs形式化为 [m*theta_0, m*theta_1, ..., m*theta_(d/2-1)],其中 m=0,1,...,length-1

    # 计算cos(m*theta)+j*sin(m*theta)
    freqs_cis = torch.polar(torch.ones_like(freqs), freqs)  # complex64
    # freqs_cis: [cos(m*theta_0)+j*sin(m*theta_0),  cos(m*theta_1)+j*sin(m*theta_1),), ..., cos(m*theta_(d/2-1))+j*sin(m*theta_(d/2-1))]
    # 其中j为虚数单位， m=0,1,...,length-1
    return freqs_cis # [length, d/2]

def reshape_for_broadcast(freqs_cis: torch.Tensor, x: torch.Tensor):
    ndim = x.ndim
    assert 0 <= 1 < ndim
    assert freqs_cis.shape == (x.shape[1], x.shape[-1])
    shape = [d if i == 1 or i == ndim - 1 else 1 for i, d in enumerate(x.shape)] # (1, length, 1, d/2)
    return freqs_cis.view(*shape) # [1, length, 1, d/2]

def apply_rotary_emb(xq: torch.Tensor, xk: torch.Tensor, freqs_cis: torch.Tensor,):
    # 先将xq维度变为[bs, length, head,  d/2, 2], 利用torch.view_as_complex转变为复数
    # xq:[q0, q1, .., q(d-1)] 转变为 xq_: [q0+j*q1, q2+j*q3, ..., q(d-2)+j*q(d-1)]
    xq_ = torch.view_as_complex(xq.float().reshape(*xq.shape[:-1], -1, 2)) # [bs, length, head, d/2]
    # 同样的，xk_:[k0+j*k1, k2+j*k3, ..., k(d-2)+j*k(d-1)]
    xk_ = torch.view_as_complex(xk.float().reshape(*xk.shape[:-1], -1, 2))

    freqs_cis = reshape_for_broadcast(freqs_cis, xq_) # [1, length, 1, d/2]
    # 下式xq_ * freqs_cis形式化输出，以第一个为例, 如下
    # (q0+j*q1)(cos(m*theta_0)+j*sin(m*theta_0)) = q0*cos(m*theta_0)-q1*sin(m*theta_0) + j*(q1*cos(m*theta_0)+q0*sin(m*theta_0))
    # 上式的实部为q0*cos(m*theta_0)-q1*sin(m*theta_0)，虚部为q1*cos(m*theta_0)+q0*sin(m*theta_0)
    # 然后通过torch.view_as_real函数，取出实部和虚部，维度由[bs, length, head, d/2]变为[bs, length, head, d/2, 2]，最后一维放实部与虚部
    # 最后经flatten函数将维度拉平，即[bs, length, head, d]
    # 此时xq_out形式化为 [实部0，虚部0，实部1，虚部1，..., 实部(d/2-1), 虚部(d/2-1)]
    xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(3) # [bs, length, head, d]
    # 即为新生成的q

    xk_out = torch.view_as_real(xk_ * freqs_cis).flatten(3)
    return xq_out.type_as(xq), xk_out.type_as(xk)

if __name__=='__main__':
    # (bs, length, head, d)
    q = torch.randn((2, 10, 12, 32))  # q=[q0, q1, .., qd-1]
    k = torch.randn((2, 10, 12, 32))
    v = torch.randn((2, 10, 12, 32))
    freqs_cis= precompute_freqs_cis(dim=32, end=10, constant= 10000.0)
    # print(freqs_cis.detach().numpy())

    q_new, k_new = apply_rotary_emb(xq=q, xk=k, freqs_cis=freqs_cis)
    print()

分组查询注意力(GQA)

从Multi-HeadAttention到Group-QueryAttention。这种技术通过将注意力机制中的查询分组，减少了计算量，同时保持了模型的性能。

RMSNorm

R M S(a)=\sqrt{\frac{1}{n} \sum_{i=1}^{n} a_{i}^{2}}

\bar{a}_{i}=\frac{a_{i}}{R M S(\boldsymbol{a})}

此外，RMSNorm 还可以引入可学习的缩放因子 𝑔𝑖和偏移参数 𝑏𝑖，从而得到

$\bar{a}{i}=\frac{a{i}}{\operatorname{RMS}(\boldsymbol{a})} g_{i}+b_{i}$ 。

RMSNorm 在 HuggingFace Transformer 库中代码实现如下所示：


class LlamaRMSNorm(nn.Module):
  def __init__(self, hidden_size, eps=1e-6): 
    """ 
    LlamaRMSNorm is equivalent to T5LayerNorm 
    """ 
    super().__init__() 
    self.weight = nn.Parameter(torch.ones(hidden_size)) 
    self.variance_epsilon = eps # eps 防止取倒数之后分母为 0 
  
  def forward(self, hidden_states): 
    input_dtype = hidden_states.dtype 
    variance = hidden_states.to(torch.float32).pow(2).mean(-1, keepdim=True) 
    hidden_states = hidden_states * torch.rsqrt(variance + self.variance_epsilon) # weight 是末尾乘的可训练参数, 即 g_i 
    
    return (self.weight * hidden_states).to(input_dtype)

layernorm:

\text{Norm}(x_i) = \frac{x_i - \mu}{\sqrt{\sigma^2 + \epsilon}}

(u均值，6方差，&偏置)

SwiGLU

SwiGLU激活函数是相较于 ReLU 函数在大部分评测中都有不少提升。

\operatorname{SwiGLU}(\boldsymbol{x}, \boldsymbol{W}, \boldsymbol{V})=\operatorname{Swish}_{\beta}(x \boldsymbol{W}) \otimes \boldsymbol{x} \boldsymbol{V}

\operatorname{Swish}_{\beta}(\boldsymbol{x})=\boldsymbol{x} \sigma(\boldsymbol{\beta} \boldsymbol{x})

$σ(x)$ 是 Sigmoid 函数，⊗表示两个向量逐元素相乘。

首先输入向量x（在下图中使用的符号是E）经过两个独立的卷积层/MLP层，得到向量A和向量B。此时，向量A和向量B的公式为：A=x⋅W+b，B=x⋅V+c。然后向量B经过一个sigmoid函数之后，σ(B)中的每个元素就都变为了0～1之间的值，就可以起到控制信息是否通过的作用。将向量A与σ(B)逐个元素相乘之后就得到了GLU层的最终输出结果，把上面描述的整个过程结合起来，GLU的公式如

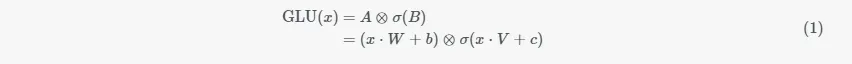
不同的𝛽的激活函数曲线：

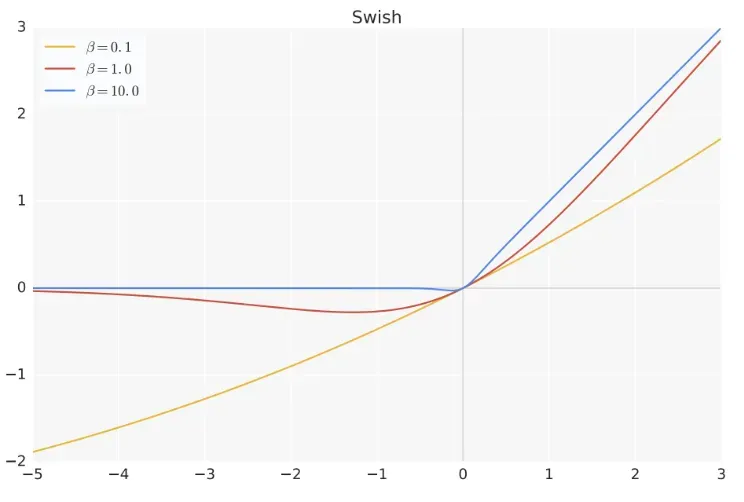
具体维度上来说，通过将维度升到8/3d，使得总参数量和原FNN的参数量一致，为4d2

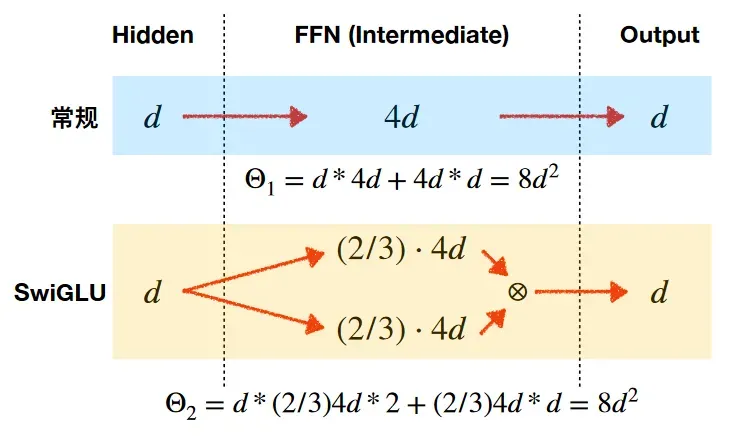
优势对比relu：

非线性更强、门控加权动态调整、梯度平滑不会梯度消失

AdamW

Adam:

Adam是改进的SGD，它加入了更新的动量和自适应的学习率，可以帮助更快地收敛。

优点：它融合了Momentum优化方法和RMSProp优化方法，可以帮助优化算法提高精度。它还可以自动调整学习率，因此不需要太多参数调整。

缺点：它需要消耗更多的内存，而且可能会出现收敛问题。

AdamW:

AdamW是Adam的变体，用来处理大型数据集，它以一定的比率来缩减模型参数的梯度，从而减少计算量，提高训练速度。

优点：它可以自动调整学习率，而不需要太多参数调整，降低了冗余性。它也可以自动调整权重衰减系数，使模型更加稳定，避免过拟合。

缺点：学习率容易受到网络噪声的影响，从而影响优化过程。

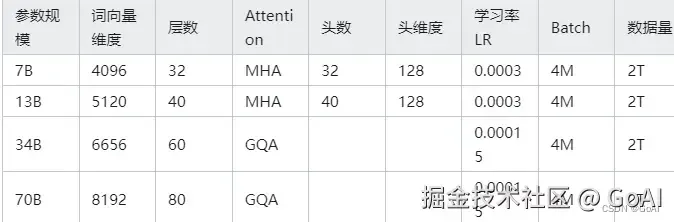
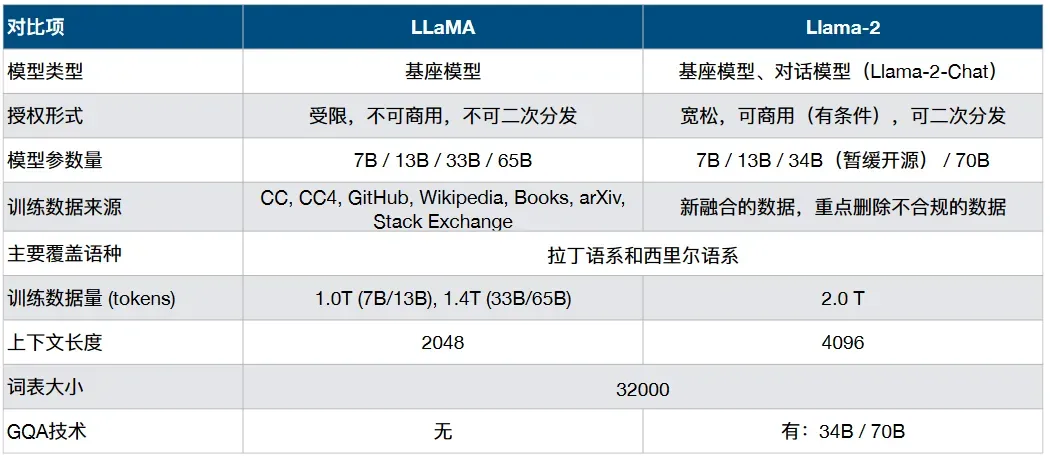
LLama家族发展史

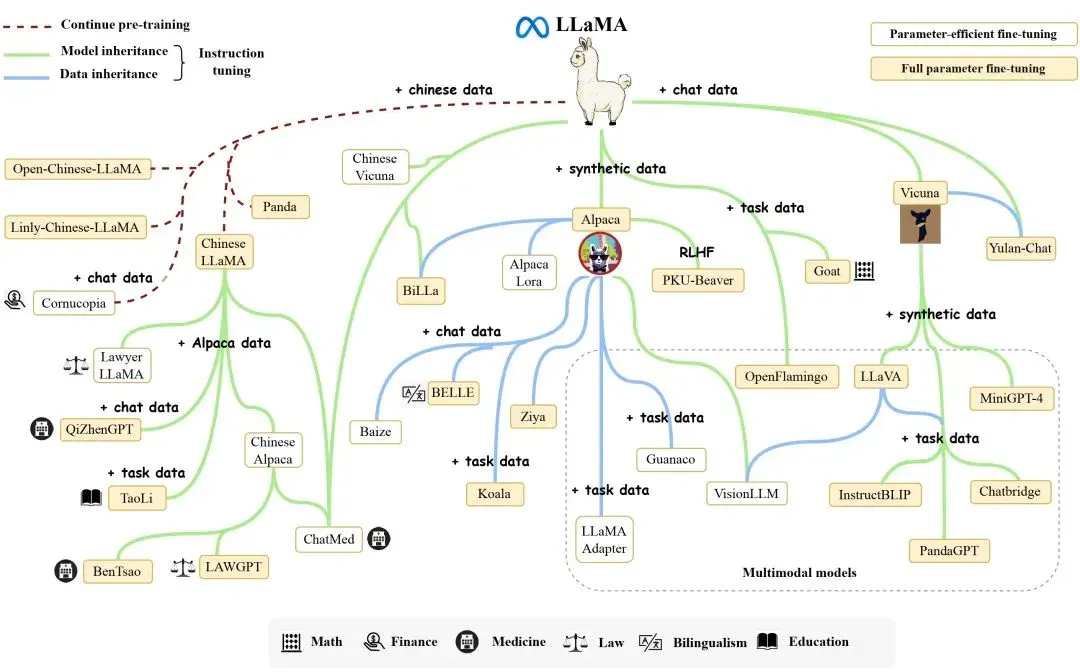
LLaMA：开源大模型繁荣发展的开端，一系列相关工作均基于LLaMA开展模型规模7B、13B、33B、65B满足了开发者和研究者的不同需求

Alpaca： 通过少量的指令精调赋予LLaMA指令理解与执行的能力

Llama-2： LLaMA的二代模型，相关模型性能进一步提升，模型可商用推出官方对⻬的Chat版本模型，采用了完整的RLHF链条

Code Llama： 专注于代码能力的LLaMA模型，最好的模型代码能力接近GPT-4效果。

Bob 的产品

1.【Bob 的 AI 成长陪伴群】门票 99/年

🔴AI 变现项目、AI 前沿技术、NLP 知识技术分享、前瞻思考、面试技巧、找工作等

🔴 个人 IP 打造、自媒体副业、向上社交、以及我的日常生活所见所闻，所思所想。

2.【一对一的一小时咨询服务】（49/次）

找一群人一起走，慢慢变富。期待和同频的朋友一起蜕变！

3.【简历指导修改】(149/人)

设计多次修改优化.发掘你的潜在价值与内容.

目录